Tutorial Teknik Digital : Teorema Boolean dan Rangkaian Kombinatorial

<strong>TEOREMA BOOLEAN

Sifat-sifat atau teorema Boolean digunakan untuk menyederhanakan fungsi-fungsi suatu untai digital. Tabel di bawah ini merupakan sifat-sifat aljabar Boolean secara umum : :2thumbup

No.	Ekspresi dan Sifat Logika	Keterangan
*Satu Variabel (Single Variable)*
1	X + 0 = X	Bound Law
2	X + 1 = 1	Bound Law
3	X . 0 = 0	Bound Law
4	X . 1 = X	Bound Law
5	X + X = X	Idempotent Law
6	X . X = X	Idempotent Law
7	X + X’ = X	Negation Law
8	X . X’ = 0	Negation Law
9	(X’)’ = X	Double Negation Law
*Dua Variabel (Two Variables)*
10	X + Y = Y + X	Commutative Law
11	X . Y = Y . X	Commutative Law
12	(X + Y)’ = X’ . Y’	De Morgan’s Law
13	(X.Y)’ = X’ + Y’	De Morgan’s Law
14	X.(X+Y) = X	Absorption Law
15	X + (X.Y) = X	Absorption Law
*Tiga Variabel (Three Variables)*
16	X+(Y+Z) = (X+Y)+Z	Associative Law
17	X.(Y.Z) = (X.Y).Z	Associative Law
18	X.(Y+Z) = X.Y + X.Z	Distributive Law
19	X + Y.Z = (X+Y) . (X+Z)	Distributive Law
20	(X+Y+Z)’ = X’ . Y’ . Z’	De Morgan’s Law
21	(X.Y.Z)’ = X’ + Y’ + Z’	De Morgan’s Law

NB : Teorema De Morgan (De Morgan’s Law) digunakan untuk menyederhanakan suatu fungsi logika yang di-invers (dikomplemenkan).

RANGKAIAN KOMBINATORIAL

Pada dasarnya rangkaian logika (digital) yang dibentuk dari beberapa gabungan komponen elektronik yang terdiri dari bermacam-macam gate dan rangkaian-rangkaian lainnya , sehingga membentuk rangkaian elektronika yang bersifat kompleks dan rumit. Untuk mengatasi hal tersebut maka dipergunakanlah beberapa penyederhanaan rangkaian logika.

Dalam penyederhanaan rangkaian logika, dapat menggunakan beberapa cara, diantaranya:

1. Metode Aljabar Boolean

Metode Aljabar Boolean merupakan suatu metode penyederhanaan rangkaian logika yang dilakukan dengan menerapkan aturan-aturan atau teorema Boolean. Metode ini lebih cepat dan mudah dibandingkan dengan menggunakan tabel kebenaran untuk menyederhanakan suatu rangkaian fungsi logika yang panjang.

2. Metode Maxterm / Minterm (Sum of Product/Product of Sum)

Metode ini selain digunakan untuk penyederhanaan suatu rangkaian logika juga dapat digunakan untuk mendesain rangkaian logika. Untuk menggunakan metode ini dikenal dua cara penyajian fungsi Boolean yaitu :

-> sukumin (singkatan dari “suku minimum” minterm, minimum term), simbol: m_n

Sum Of Product (SOP), nilai 1

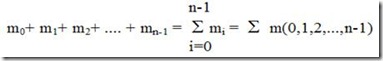Bentuk rangkaian SOP ini terdiri dari sekumpulan gerbang AND yang diumpankan

ke sebuah gerbang OR.

Prosedur desain dengan metode SOP (Sum of Product) :

1. Menentukan tabel kebenaran

2. Menulis minterm (ANDterm) dari masing-masing kombinasi input yang menghasilkan output 1

3. Menulis persamaan SOP sebagai persamaan outputnya

4. Menyederhanakan persamaan output tersebut

5. Menggambarkan rangkaian dari hasil step 4

-> sukumax (singkatan dari “suku maksimum” maxterm, maximum term), simbol: M_n

Product of sum (POS), nilai 0

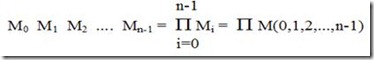Rangkaiannya akan terdiri dari sekumpulan gerbang OR yang diumpankan ke sebuah gerbang AND.

Prosedur desain dengan metode POS (Product of Sum) :

1. Menentukan tabel kebenaran

2. Menulis maxterm (ORterm) dari masing-masing kombinasi input yang menghasilkan output 0

3. Menulis persamaan POS sebagai persamaan outputnya

4. Menyederhanakan persamaan output tersebut

5. Menggambarkan rangkaian dari hasil step 4

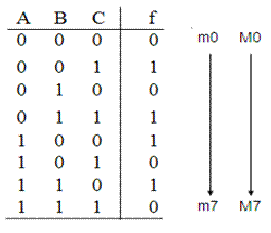
Contoh untuk kedua metode di atas :

SOP : = m1 + m3 + m4 +m6

POS : = M0 + M2 + M5 + M7

3. Metode Karnaugh Map

Metode Karnaugh Map merupakan salah satu cara untuk menyederhanakan fungsi Boolean yaitu dengan memetakan tabel kebenaran dalam kotak-kotak segi empat yang jumlahnya tergantung dari jumlah peubah (variabel) masukan. Peta Karnaugh juga dapat digunakan untuk menilik kesamaan dua buah fungsi Boolean. Metode Karnaugh Map ada dua cara :

Ø Karnaugh Map Sukumin

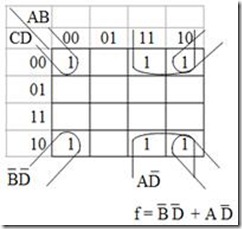
Merupakan penyederhanaan untuk setiap “1” yang bertetanggaan 2,4,8,16… menjadi suku minterm yang sederhana.

Contoh : f = S m (0,2,8,10,12,14 )

Ø Karnaugh Map Sukumax

Merupakan penyederhanaan untuk setiap “0” yang bertetanggaan 2,4,8,16… menjadi suku maxterm yang sederhana. Prosedur yang dilakukan untuk menggunakan metode ini sama seperti pada metode Karnaugh Map Sukumin, yang membedakan hanya dalam hal jenis suku yang diambil saat penyederhanaan yaitu suku maxterm.

Komentar