#BelajarPython 3: Faktorisasi Prima Sebuah Bilangan

Jika pada artikel saya sebelumnya, saya menuliskan kode program untuk menentukan bilangan prima dan faktor sebuah bilangan, maka pada artikel saya kali ini akan membahas sedikit lebih jauh tentang faktorisasi prima.

Faktorisasi prima adalah pecahan bilangan komposit yang terdiri dari bilangan-bilangan pembagi yang lebih kecil, dan hasil perkalian dari bilangan-bilangan tersebut sama dengan bilangan komposit yang disebutkan.

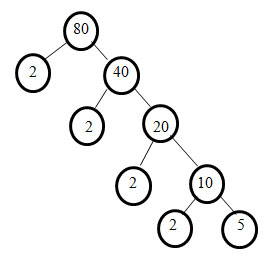
Contoh faktorisasi prima dari bilangan 80 bisa dilihat pada gambar berikut. Bilangan 2 dan 5 merupakan bilangan prima yang merupakan bilangan pembagi dari 80.

Teori tentang faktorisasi prima tentunya sudah diajarkan sejak sekolah dasar. Namun, contoh penerapan sebenarnya dalam dunia komputasi yaitu digunakan untuk mengembangkan algoritma kriptografi RSA.

Algoritma RSA termasuk jenis algoritma enkripsi yang sulit dipecahkan karena hingga saat ini belum ditemukan algoritma yang mampu memecahkan masalah faktorisasi dalam waktu polinomial.

Algoritma menentukan faktorisasi prima sebuah bilangan:

1. Masukkan bilangan yang akan diuji, misal diwakili dengan variabel angka.
2. Cek bilangan diuji dengan cara membagi bilangan tersebut dengan bilangan pembagi, yang dimulai dari bilangan 2 hingga bilangan angka.
3. Jika tak ada sisa (ditentukan dengan operasi modulo) maka simpan bilangan pembagi tersebut.
4. Tampilkan semua bilangan pembagi ke dalam format array.

Kode program faktorisasiprima.py:

# fungsi untuk mencari faktorisasi prima sebuah bilangan
def faktorisasiprima(x):
    # keluaran variabel factorlist berupa array
    factorlist=[]
    loop=2
    while loop<=x:
        if x%loop==0:
            x/=loop
            # append berfungsi untuk menambahkan sebuah objek ke dalam list/daftar
            factorlist.append(loop)
        else:
            loop+=1
    return factorlist

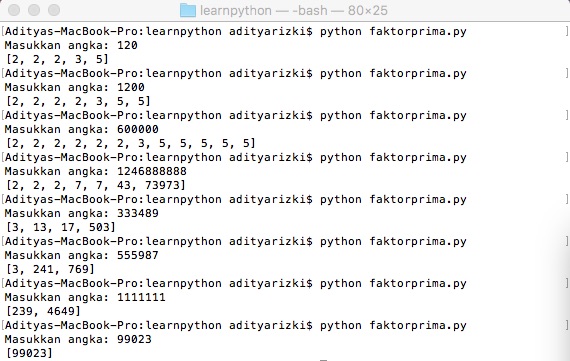
angka = int(input("Masukkan angka: "))
print faktorisasiprima(angka)

Hasil eksekusi program: